The Vorbis audio CODEC provides a channel coupling mechanisms designed to reduce effective bitrate by both eliminating interchannel redundancy and eliminating stereo image information labeled inaudible or undesirable according to spatial psychoacoustic models. This document describes both the mechanical coupling mechanisms available within the Vorbis specification, as well as the specific stereo coupling models used by the reference libvorbis codec provided by xiph.org.
In encoder release beta 4 and earlier, Vorbis supported multiple channel encoding, but the channels were encoded entirely separately with no cross-analysis or redundancy elimination between channels. This multichannel strategy is very similar to the mp3's dual stereo mode and Vorbis uses the same name for its analogous uncoupled multichannel modes.
However, the Vorbis spec provides for, and Vorbis release 1.0 rc1 and later implement a coupled channel strategy. Vorbis has two specific mechanisms that may be used alone or in conjunction to implement channel coupling. The first is channel interleaving via residue backend type 2, and the second is square polar mapping. These two general mechanisms are particularly well suited to coupling due to the structure of Vorbis encoding, as we'll explore below, and using both we can implement both totally lossless stereo image coupling [bit-for-bit decode-identical to uncoupled modes], as well as various lossy models that seek to eliminate inaudible or unimportant aspects of the stereo image in order to enhance bitrate. The exact coupling implementation is generalized to allow the encoder a great deal of flexibility in implementation of a stereo or surround model without requiring any significant complexity increase over the combinatorially simpler mid/side joint stereo of mp3 and other current audio codecs.
A particular Vorbis bitstream may apply channel coupling directly to more than a pair of channels; polar mapping is hierarchical such that polar coupling may be extrapolated to an arbitrary number of channels and is not restricted to only stereo, quadraphonics, ambisonics or 5.1 surround. However, the scope of this document restricts itself to the stereo coupling case.
Recall that the basic structure of a a Vorbis I stream first generates from input audio a spectral 'floor' function that serves as an MDCT-domain whitening filter. This floor is meant to represent the rough envelope of the frequency spectrum, using whatever metric the encoder cares to define. This floor is subtracted from the log frequency spectrum, effectively normalizing the spectrum by frequency. Each input channel is associated with a unique floor function.
The basic idea behind any stereo coupling is that the left and right channels usually correlate. This correlation is even stronger if one first accounts for energy differences in any given frequency band across left and right; think for example of individual instruments mixed into different portions of the stereo image, or a stereo recording with a dominant feature not perfectly in the center. The floor functions, each specific to a channel, provide the perfect means of normalizing left and right energies across the spectrum to maximize correlation before coupling. This feature of the Vorbis format is not a convenient accident.
Because we strive to maximally correlate the left and right channels and generally succeed in doing so, left and right residue is typically nearly identical. We could use channel interleaving (discussed below) alone to efficiently remove the redundancy between the left and right channels as a side effect of entropy encoding, but a polar representation gives benefits when left/right correlation is strong.
The first advantage of a polar representation is that it effectively separates the spatial audio information into a 'point image' (magnitude) at a given frequency and located somewhere in the sound field, and a 'diffuse image' (angle) that fills a large amount of space simultaneously. Even if we preserve only the magnitude (point) data, a detailed and carefully chosen floor function in each channel provides us with a free, fine-grained, frequency relative intensity stereo*. Angle information represents diffuse sound fields, such as reverberation that fills the entire space simultaneously.
*Because the Vorbis model supports a number of different possible stereo models and these models may be mixed, we do not use the term 'intensity stereo' talking about Vorbis; instead we use the terms 'point stereo', 'phase stereo' and subcategories of each.
The majority of a stereo image is representable by polar magnitude alone, as strong sounds tend to be produced at near-point sources; even non-diffuse, fast, sharp echoes track very accurately using magnitude representation almost alone (for those experimenting with Vorbis tuning, this strategy works much better with the precise, piecewise control of floor 1; the continuous approximation of floor 0 results in unstable imaging). Reverberation and diffuse sounds tend to contain less energy and be psychoacoustically dominated by the point sources embedded in them. Thus, we again tend to concentrate more represented energy into a predictably smaller number of numbers. Separating representation of point and diffuse imaging also allows us to model and manipulate point and diffuse qualities separately.
Because polar representation concentrates represented energy into fewer large values, we reduce bit 'leakage' during cascading (multistage VQ encoding) as a secondary benefit. A single large, monolithic VQ codebook is more efficient than a cascaded book due to entropy 'crosstalk' among symbols between different stages of a multistage cascade. Polar representation is a way of further concentrating entropy into predictable locations so that codebook design can take steps to improve multistage codebook efficiency. It also allows us to cascade various elements of the stereo image independently.
Rounding and computational complexity are potential problems with a polar representation. As our encoding process involves quantization, mixing a polar representation and quantization makes it potentially impossible, depending on implementation, to construct a coupled stereo mechanism that results in bit-identical decompressed output compared to an uncoupled encoding should the encoder desire it.
Vorbis uses a mapping that preserves the most useful qualities of polar representation, relies only on addition/subtraction (during decode; high quality encoding still requires some trig), and makes it trivial before or after quantization to represent an angle/magnitude through a one-to-one mapping from possible left/right value permutations. We do this by basing our polar representation on the unit square rather than the unit-circle.
Given a magnitude and angle, we recover left and right using the following function (note that A/B may be left/right or right/left depending on the coupling definition used by the encoder):
if(magnitude>0)
if(angle>0){
A=magnitude;
B=magnitude-angle;
}else{
B=magnitude;
A=magnitude+angle;
}
else
if(angle>0){
A=magnitude;
B=magnitude+angle;
}else{
B=magnitude;
A=magnitude-angle;
}
}
The function is antisymmetric for positive and negative magnitudes in order to eliminate a redundant value when quantizing. For example, if we're quantizing to integer values, we can visualize a magnitude of 5 and an angle of -2 as follows:
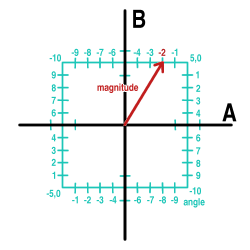
This representation loses or replicates no values; if the range of A and B are integral -5 through 5, the number of possible Cartesian permutations is 121. Represented in square polar notation, the possible values are:
0, 0 -1,-2 -1,-1 -1, 0 -1, 1 1,-2 1,-1 1, 0 1, 1 -2,-4 -2,-3 -2,-2 -2,-1 -2, 0 -2, 1 -2, 2 -2, 3 2,-4 2,-3 ... following the pattern ... ... 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5, 7 5, 8 5, 9
...for a grand total of 121 possible values, the same number as in Cartesian representation (note that, for example, 5,-10 is the same as -5,10, so there's no reason to represent both. 2,10 cannot happen, and there's no reason to account for it.) It's also obvious that this mapping is exactly reversible.
We can remap and A/B vector using polar mapping into a magnitude/angle vector, and it's clear that, in general, this concentrates energy in the magnitude vector and reduces the amount of information to encode in the angle vector. Encoding these vectors independently with residue backend #0 or residue backend #1 will result in bitrate savings. However, there are still implicit correlations between the magnitude and angle vectors. The most obvious is that the amplitude of the angle is bounded by its corresponding magnitude value.
Entropy coding the results, then, further benefits from the entropy model being able to compress magnitude and angle simultaneously. For this reason, Vorbis implements residue backend #2 which pre-interleaves a number of input vectors (in the stereo case, two, A and B) into a single output vector (with the elements in the order of A_0, B_0, A_1, B_1, A_2 ... A_n-1, B_n-1) before entropy encoding. Thus each vector to be coded by the vector quantization backend consists of matching magnitude and angle values.
The astute reader, at this point, will notice that in the theoretical case in which we can use monolithic codebooks of arbitrarily large size, we can directly interleave and encode left and right without polar mapping; in fact, the polar mapping does not appear to lend any benefit whatsoever to the efficiency of the entropy coding. In fact, it is perfectly possible and reasonable to build a Vorbis encoder that dispenses with polar mapping entirely and merely interleaves the channel. Libvorbis based encoders may configure such an encoding and it will work as intended.
However, when we leave the ideal/theoretical domain, we notice that polar mapping does give additional practical benefits, as discussed in the above section on polar mapping and summarized again here:
Dual stereo refers to stereo encoding where the channels are entirely separate; they are analyzed and encoded as entirely distinct entities. This terminology is familiar from mp3.
Using polar mapping and/or channel interleaving, it's possible to couple Vorbis channels losslessly, that is, construct a stereo coupling encoding that both saves space but also decodes bit-identically to dual stereo. OggEnc 1.0 and later uses this mode in all high-bitrate encoding.
Overall, this stereo mode is overkill; however, it offers a safe alternative to users concerned about the slightest possible degradation to the stereo image or archival quality audio.
Phase stereo is the least aggressive means of gracefully dropping resolution from the stereo image; it affects only diffuse imaging.
It's often quoted that the human ear is deaf to signal phase above about 4kHz; this is nearly true and a passable rule of thumb, but it can be demonstrated that even an average user can tell the difference between high frequency in-phase and out-of-phase noise. Obviously then, the statement is not entirely true. However, it's also the case that one must resort to nearly such an extreme demonstration before finding the counterexample.
'Phase stereo' is simply a more aggressive quantization of the polar angle vector; above 4kHz it's generally quite safe to quantize noise and noisy elements to only a handful of allowed phases, or to thin the phase with respect to the magnitude. The phases of high amplitude pure tones may or may not be preserved more carefully (they are relatively rare and L/R tend to be in phase, so there is generally little reason not to spend a few more bits on them)
Vorbis may implement phase stereo coupling by preserving the entirety of the magnitude vector (essential to fine amplitude and energy resolution overall) and quantizing the angle vector to one of only four possible values. Given that the magnitude vector may be positive or negative, this results in left and right phase having eight possible permutation, thus 'eight phase stereo':
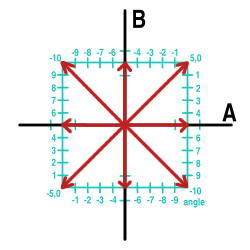
Left and right may be in phase (positive or negative), the most common case by far, or out of phase by 90 or 180 degrees.
Similarly, four phase stereo takes the quantization one step further; it allows only in-phase and 180 degree out-out-phase signals:
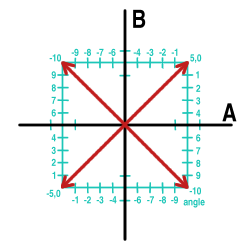
Point stereo eliminates the possibility of out-of-phase signal entirely. Any diffuse quality to a sound source tends to collapse inward to a point somewhere within the stereo image. A practical example would be balanced reverberations within a large, live space; normally the sound is diffuse and soft, giving a sonic impression of volume. In point-stereo, the reverberations would still exist, but sound fairly firmly centered within the image (assuming the reverberation was centered overall; if the reverberation is stronger to the left, then the point of localization in point stereo would be to the left). This effect is most noticeable at low and mid frequencies and using headphones (which grant perfect stereo separation). Point stereo is is a graceful but generally easy to detect degradation to the sound quality and is thus used in frequency ranges where it is least noticeable.
Mixed stereo is the simultaneous use of more than one of the above stereo encoding models, generally using more aggressive modes in higher frequencies, lower amplitudes or 'nearly' in-phase sound.
It is also the case that near-DC frequencies should be encoded using lossless coupling to avoid frame blocking artifacts.
Vorbis, as of 1.0, uses lossless stereo and a number of mixed modes constructed out of lossless and point stereo. Phase stereo was used in the rc2 encoder, but is not currently used for simplicity's sake. It will likely be re-added to the stereo model in the future.